Spot-On documentation
The official Spot-On documentation.
Spot-On allows you to analyze single particle tracking datasets. Spot-On fits a realistic kinetic model to the distribution of jump lengths and provides estimates of the fraction bound (\(F\)) and diffusion coefficients (\(D\)) for either a two state (bound-free) or a three state (bound-free1-free2) model.
Spot-On is a libre/open-source software and exists both as a web-application and a command-line version.

Browse the documentation for various versions of Spot-On:
The problem
Within a cell, a DNA-binding factor diffuses and occasionnally binds to DNA or forms complexes. Each of this state can be macroscopically characterized by an apparent diffusion coefficient and a fraction of the total population residing in this state. Thus, we are interested into extracting those parameters for each state.
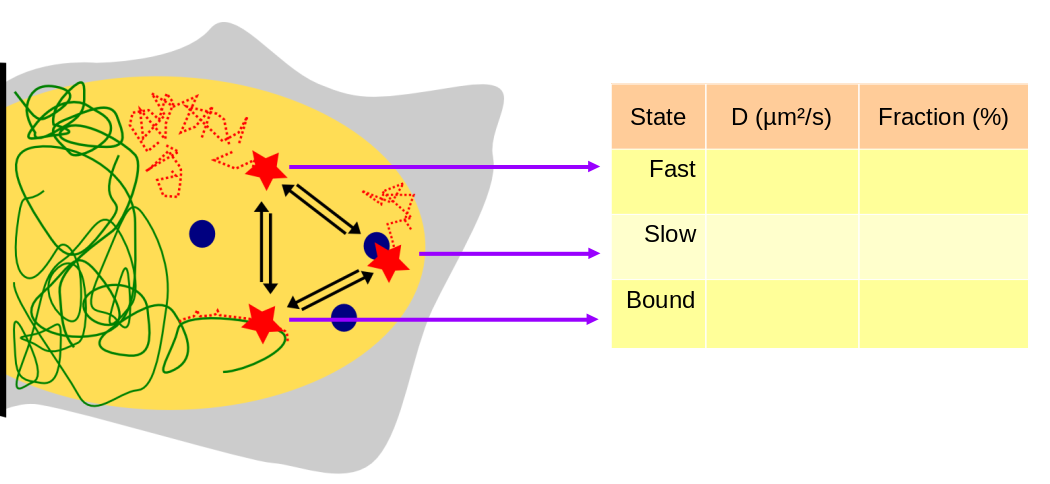
To infer those parameters, single particle tracking can be used, but is subject to several methodological difficulties detailed below.
Motion blur
First of all, observation and tracking are biased towards bound and undercounting of the fast-moving particles, and second in a possible bias in the estimate of the free fraction.
Particles move out of focus
In addition to motion blur, that leads to fast-moving particle to be missed by the detection algorithm, particles diffuse out of the detection volume (usually a slice of ~ 1 µm thickness). This effect is virtually zero for bound molecule, but becomes significant for fast-moving particles, leading to an undercounting of this population. The animated graph below shows the distribution of jump lengths for a molecule appearing in two states with respective diffusion coefficients \(D_1\) and \(D_2\).
| D1 (μm²/s) | |
| D2 (μm²/s) | |
| P | |
| σ (nm) | |
| Δt (ms) | |
| Show model with no depth of field correction |
|
From this representation, the fraction of particles lost can be determined as a function of the diffusion coefficient and the exposure time. This emphasizes the difficulty to capture fast-moving particles (\(D> 5 \mu m/s\)), even at low exposure times.

Ambiguous tracking
As single particle tracking is intrinsically a low-throughput method, one may want to increase the density of tracked particles per frame in order to accelerate the data collection rate. However, as the density of particles increases, the tracking can become ambiguous. Furthermore, fast-moving particles are again more likely to be misconnected with other unrelated detections. This might result in a truncated jump length distribution, and thus a wrong estimation of the diffusion coefficient.
Quickstart/tutorial
This section of the Spot-On documentation will guide you through a sample analysis with a couple of demonstration files and will provide you with an overview of Spot-On features and options.
Step 1: start an analysis with demonstration files
To access the demonstration files, go to the Spot-On homepage and scroll to the "Get Started section" (or alternatively click the Start spotting! button on the top menu. First fill in the "I'm not a robot" CAPTCHA. Then you have the option to either upload your own tracking files and start your analysis or start with demo files. We choose this later option for the purpose of this tutorial.
This option will load the analysis page and will automatically import some demonstration file. Also, a custom and permanent URL is created. Your analyses will accessible from this URL until you choose to delete them. Do not share this URL if you want your datasets and analyses to remain private. You might want to bookmark it in order to reaccess the data later. Note that if you lose this address, there is no way for you to recover your files, since your upload is totally anonymous (we do not collect your identity or email address).
Overview of the application
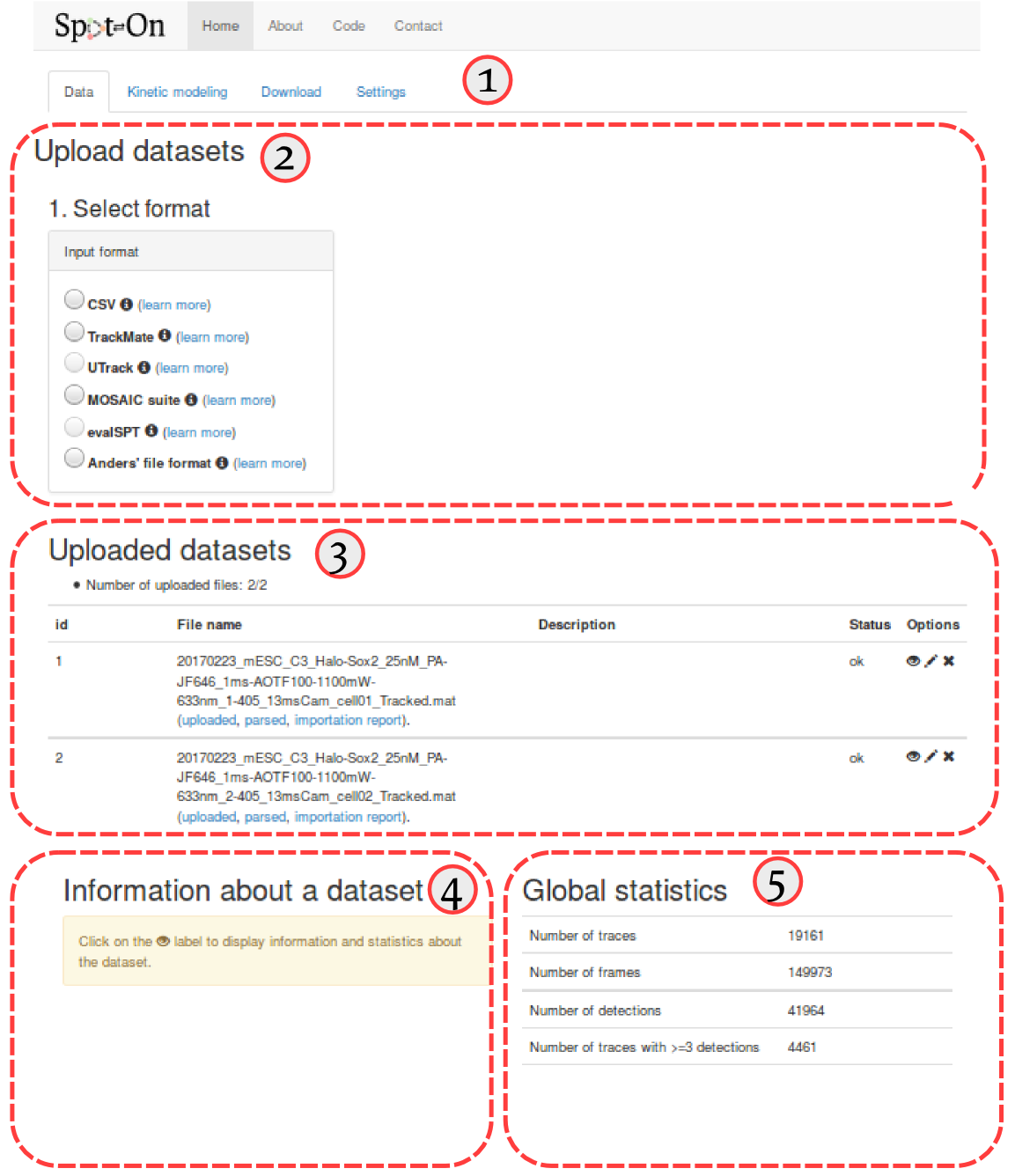
First of all, Spot-On is organized into four successive tabs. These tabs are populated one after the other (that is, for instance, the "Kinetic modeling" tab remains blank as long as no dataset has been uploaded in the "Data" tab, etc). The four tabs are (① in the screenshot below):
| Tab | Description |
|---|---|
| Data | This tab allows you to upload your datasets in various formats in a batch mode, to annotate them, and to see statistics both for individual datasets and for the ensemble of uploaded files. |
| Kinetic modeling | Performs the fit of the kinetic model according to specified parameters, display the jump length distribution and the corresponding fit. Allows to include or exclude files for analysis. Display and fits can be marked for download. |
| Download | Allows to download the files marked for download in various formats (PDF, SVG, EPS, PNG, and ZIP archive). The ZIP archive contains the raw data, the fitting parameters and the fitted coefficients. |
| Settings | Allows to erase the analysis (together with all the uploaded datasets). |
The "Upload dataset" region (② in the screenshot below), where you can upload from various file formats. Clicking on any of the format will display a box where you can enter additional upload parameters, and will ultimately display a drag-and-drop upload box. Accepted formats are described in more details in the Input formats section below.
The "Uploaded datasets" region (③ in the screenshot below), that displays the uploaded datasets, together with their status (uploading, queued, error). The meaning of the upload codes is detailed in the Import codes section below. When clicking on the "eye" symbol () next to an uploaded dataset will display some statistics in the area ④. The meaning and details of the computation of each statistic is detailed in section Dataset statistics below. Finally, area ⑤ displays similar statistics as area ④, but for all the datasets pooled together.
Import
To proceed with the tutorial, several files have been loaded, they are named:
- 20170223_mESC_C3_Halo-Sox2_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_1-405_13msCam_cell01_Tracked.mat
- 20170223_mESC_C3_Halo-Sox2_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_2-405_13msCam_cell02_Tracked.mat
- 20170223_mESC_C3_Halo-Sox2_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_1-405_13msCam_cell02_Tracked.mat
- 20170223_mESC_C3_Halo-Sox2_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_2-405_13msCam_cell03_Tracked.mat
- 20170223_mESC_C3_Halo-Sox2_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_3-405_13msCam_cell04_Tracked.mat
- 20170223_U2OS_H2b-Halo-SNAP_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_1-5-405_13msCam_cell01_Tracked.mat
- 20170223_U2OS_H2b-Halo-SNAP_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_1-7-405_13msCam_cell03_Tracked.mat
- 20170223_U2OS_H2b-Halo-SNAP_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_1-7-405_13msCam_cell02_Tracked.mat
- 20170307_U2OS_H2b-Halo-SNAP_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_1-5-405_13msCam_cell03_Tracked.mat
- 20170307_U2OS_H2b-Halo-SNAP_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_1-7-405_13msCam_cell05_Tracked.mat
These files correspond to a subset of an experimental series spanning ~1500 cells in several conditions for various transcription factors and DNA-binding proteins, acquired at various framerates and durations of stroboscopic illumination. This dataset is described in more details in the Datasets section.
Five of these correspond to the transcription factor Sox2 is endogeneously tagged with a HaloTag and observed with the PA-JF646add reference organic dye. Five other correspond to the observation of histone H2B.
Step 2: rename and tag the uploaded files
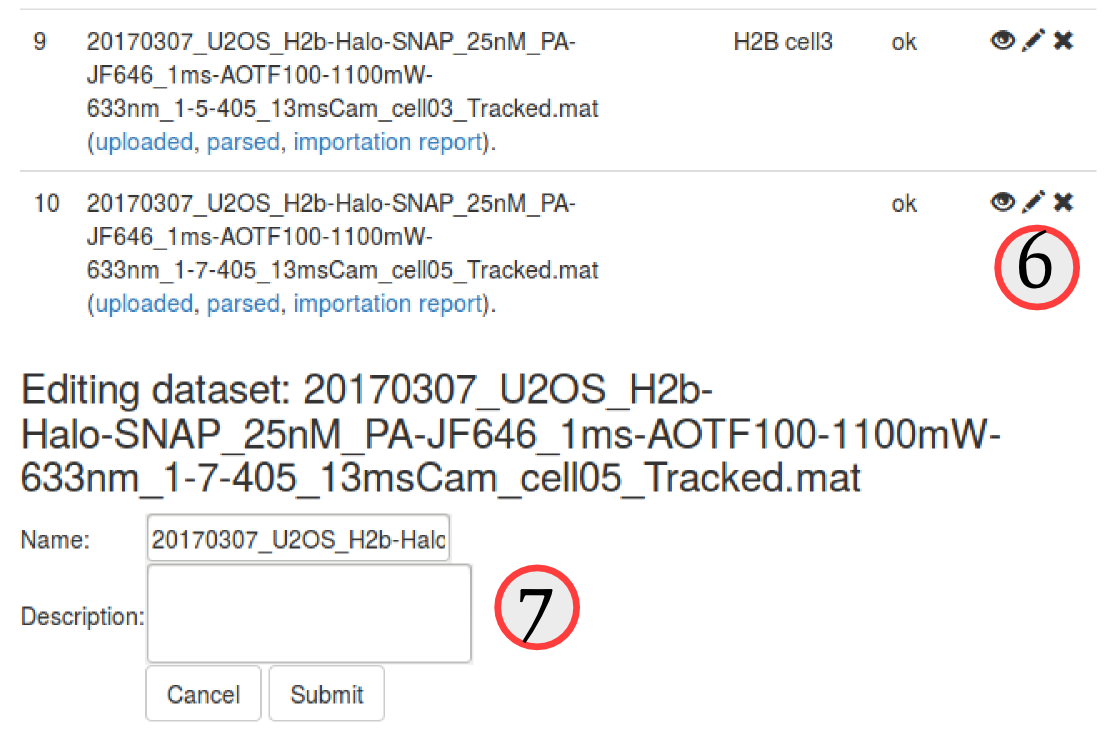
Since the naming convention of these files is a little bit cumbersome, let's first edit the description of each file to make it clearer. To do so, click on the "pencil" icon (, see ⑥) next to each uploaded dataset. An "edit" box will appear at the bottom of the "Uploaded datasets" area, and we can now either rename or add a more explicit description of the datasets. We choose to leave the name as is, but add a short description for each dataset, such as "H2B cell1", "H2B cell2", etc. (⑦)
Quality check
Now that we see a little bit clearer through the datasets, let's inspect a little bit the datasets, and try to assess the quality of the dataset. Spot-On provides a few quality metrics (statistics), accessible for each dataset by clicking the "eye" button ().
Step 3: Inspect a few quality metrics
Click on the "eye" button () next to the datasets and have a look at the metrics displayed. Make sure you familiarize yourself with those.
The table below summarizes the statistics computed for the first dataset (names 20170223_mESC_C3_Halo-Sox2_25nM_PA-JF646_1ms-AOTF100-1100mW-633nm_1-405_13msCam_cell01_Tracked.mat.
| Statistic | Value |
|---|---|
| Number of traces | 3764 |
| Number of frames | 30000 |
| Number of detections | 7625 |
| Number of traces with >=3 detections | 783 |
| Number of jumps | 3861 |
| Length of trajectories (in number of frames) | median: 1, mean: 2.026 |
| Particles per frame | median: 0, mean: 0.254 |
| Jump length (µm) | median: 0.191, Mean: 0.306 |
Comment on the main features of the dataset. Although the number of jumps is not extremely high, we need to keep in mind that we plan to pool this dataset with four other datasets, which should overcome the limited size of this dataset. In case we encounter a dataset of unsuitable quality, we can exclude it by clicking the "cross" button () next to the dataset.
Once that we are confident about the quality of the uploaded data, we can proceed to the second tab, the "Kinetic modeling".
Kinetic modeling
Overview of the kinetic modeling tab
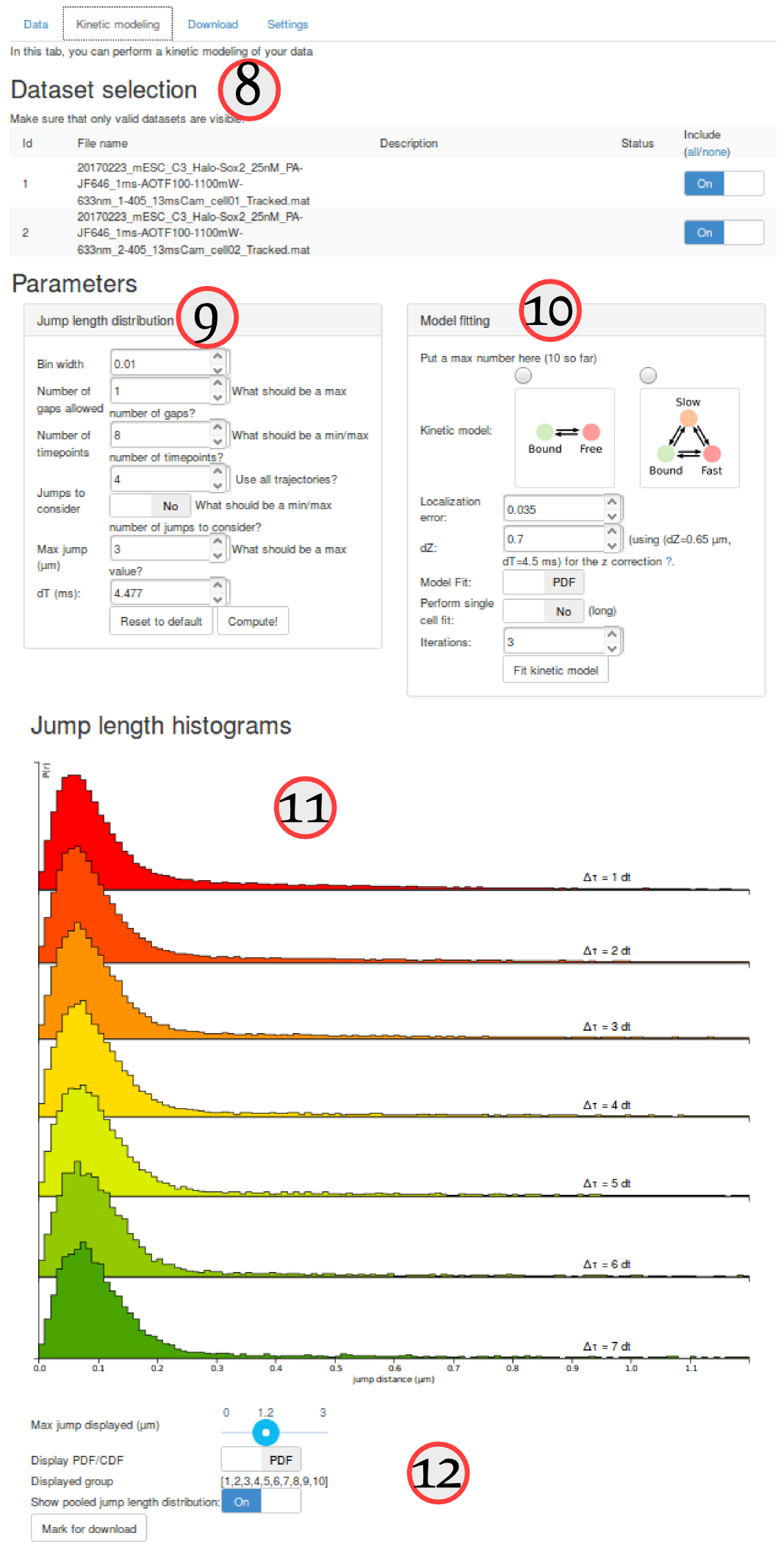
The "kinetic modeling" tab is divided in several sections:
| # | Section | Description |
|---|---|---|
| ⑧ | Dataset selection | This section lists all the uploaded datasets. For each fit of the model, you can choose whether to include one specific dataset for fitting or not. |
| ⑨ and ⑩ | Parameters | Parameters used to compute the empirical jump length distribution (⑨) and to fit it (⑨). This includes the choice of a 2-states vs. a 3-states model, the range of the tested parameters, etc. |
| ⑪ and ⑫ | Jump length histogram | This area contains the plot of the jump length distribution, overlayed with the fitted model (if evaluated). It also contains option to either visualize single datasets or the pool of the selected datasets. Finally, it contains an option to save an analysis for download. |
Computation of the jump length distribution
For the purpose of this tutorial, we'll simply fit the H2B and Sox2 datasets separately, and compare the two-states and three-states models based on their goodness of fit (assessed by the Bayesian Information Criterion, BIC).
Step 4: compute the empirical jump length distribution for the Sox2 datasets
First, in the "Dataset selection" select the five Sox2 replicates. This is done by switching the "Include" toggle button to "On" next to the Sox2 datasets. Make sure that none of the H2B datasets are included.
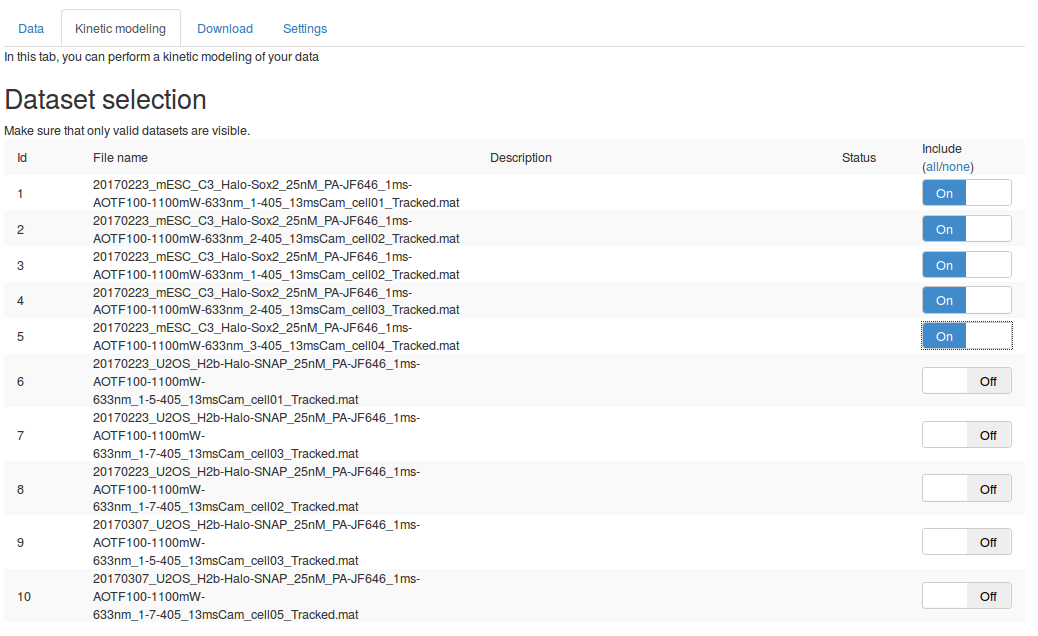
We can then set the parameters to compute the jump length distribution. We will mostly leave the parameters as default. Section Jump length distribution computation parameters describe the role of each parameter in more details.
Then click the Compute! button. After a few seconds, the jump length distribution is computed for all the datasets and appears under the "Jump length distribution" section.
The table below summarizes some key principles to properly set those parameters
| Parameter | Value | Default? | Comment |
|---|---|---|---|
| Bin Width (µm) | 0.01 | Y | The size of the bin used to build the empirical histogram of jump lengths. |
| Number of gaps allowed | 1 | Y | The number of gaps allowed by the tracking algorithm. This has to match the maximum number of gaps allowed by the tracking algorithm. |
| Number of timepoints | 8 | Y | The number of \(\Delta t\) to consider when fitting the model. Usually, higher values provide better results, provided that the histogram are sufficiently populated. |
| Jumps to consider | 4 | Y | The number of jumps per trajectory to consider. This is done to avoid overcounting bound molecules. |
| Max jump (µm) | 3 | Y | The range of distances to build the histogram of jump lengths. This parameter has to be set so that the tail of the distribution is properly captured. Conversely, a value too high will disturb the fitting, that will be very sensitive to this potentially noisy tail. |
| dT (ms) | 13 | N | It is crucial to match this value with the acquisition rate of the dataset. Here 13 ms/frame. |
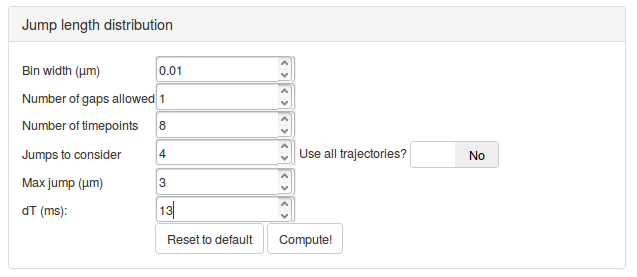
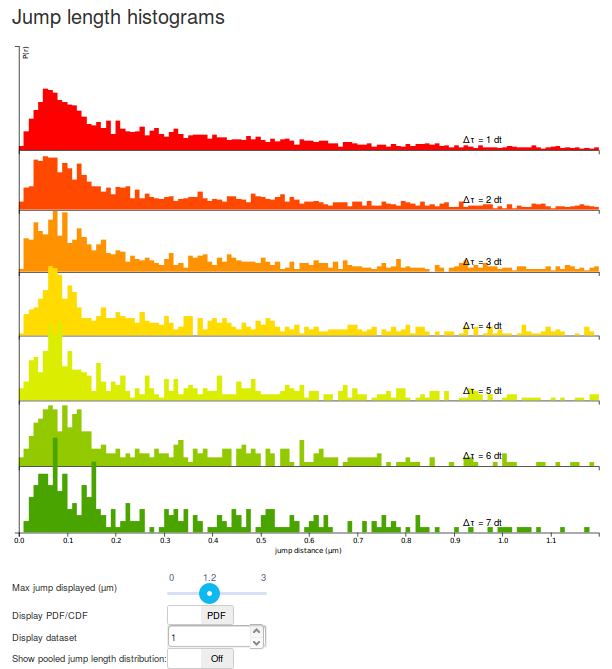
Step 5: play with the display options
The graph displayed should be read as follows:
- Each row corresponds to a jump length distribution evaluated at a given \(\Delta t\). Since short trajectories are more frequent than long trajectories, higher \(\Delta t\) histograms tend to be less populated and appear less smooth (or more "noisy"). The number of rows is determined by the "Number of timepoints" parameter.
- The jump length distribution is computed for values ranging between 0 µm and 3 µm (this corresponds to the "Max Jump" parameter). However, by default, only the first 1.2 µm are initially plotted. To plot the full histogram (or alternatively, to zoom to the origin), the "Max Jump displayed" cursor, located under the plot can be adjusted.
- Then, by default, the jump length distribution is displayed for individual datasets. The displayed dataset is specified in the "Display dataset" box under the plot. It is often useful to take the time to review the jump length distribution of each single acquisition, in order to know which datasets might have to be excluded from further analysis.
- Once individual datasets have been reviewed, it is possible to display the pooled jump length distribution by clicking the "Show pooled jump length distribution" toggle button under the plot. This will compute the distribution for the selected datasets only (in our case, for all the Sox2 datasets). Pooled histograms appear with a hard, black boundary, and the included datasets are displayed under the graph. The updated graph might take a few seconds to render.
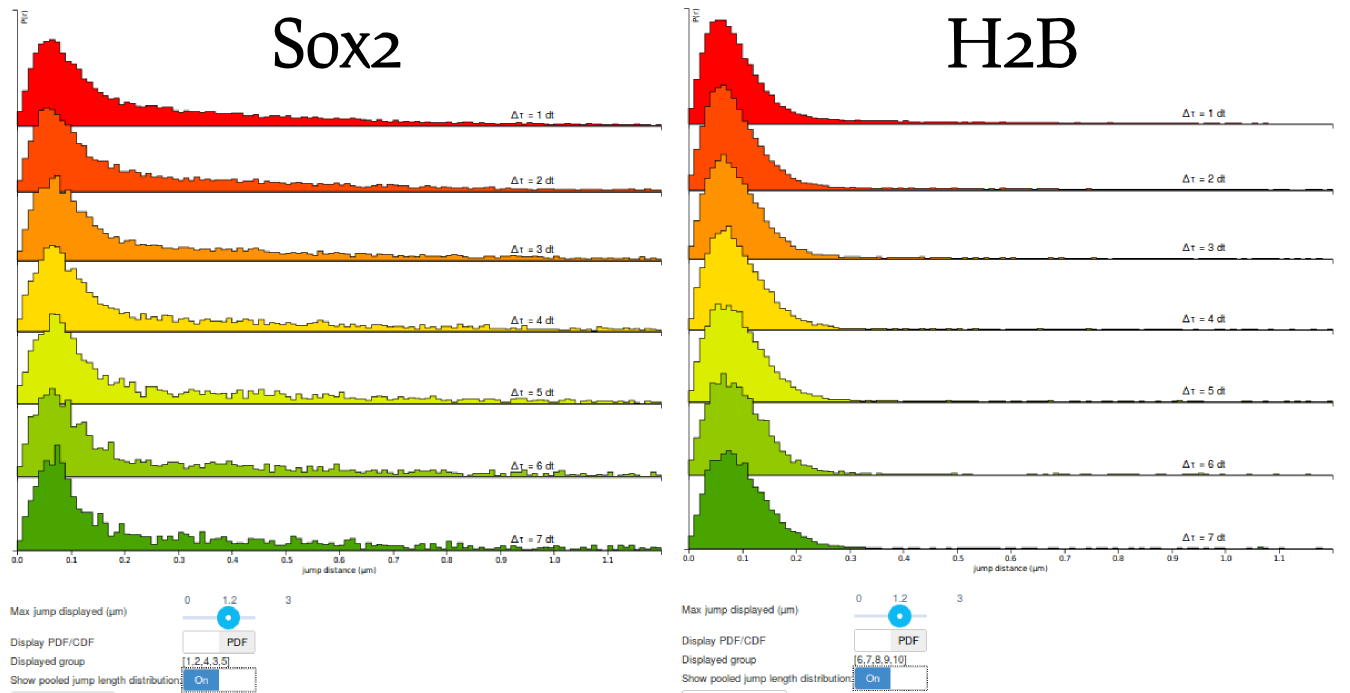
Step 6: compare the H2B and Sox2 jump length distributions
Before moving to the fitting, compare the pooled jump length distribution for Sox2 and H2B. To compute the H2B jump length distribution, simply uncheck the Sox2 datasets and select the H2B datasets in the "Dataset selection" area. Then click the Compute! button in the "Jump length distribution parameters" box. The two histograms are displayed below. What can you tell from that? Does it match your knowledge of H2B and Sox2?
Step 7: mark one jump length distribution for download
Before moving to the fitting of the data, let's save this last plot. We will download it later (from the "Download" tab). To do so, click the Mark for download button at the bottom of the page. This will prompt a small form where you can enter a name and a description that will be used as a reminder when you download the file. Also, display again the fit for Sox2 (by selecting the appropriate files and clicking the and Compute! button in the "Jump length distribution parameters" box) and save Mark it for download too. We'd get back to these saved analyses later.
Model fitting
Now that we are familiar with the computation and display of the jump length distribution, let's now move to model fitting!
Spot-On fits the jump length distribution, as defined by the parameters of the "Jump length distribution" box. The fitting parameters are defined in the "Model fitting" box.
Step 8: fit a two-states model
Let's first try to fit a two-states model. Click on the picture of the two-states kinetic model (Bound-Free). Specific parameter for this model unfold. Let's take a minute to quickly review them (a more detailed description of each parameter is presented in Section Fitting parameters, a short description is shown below).
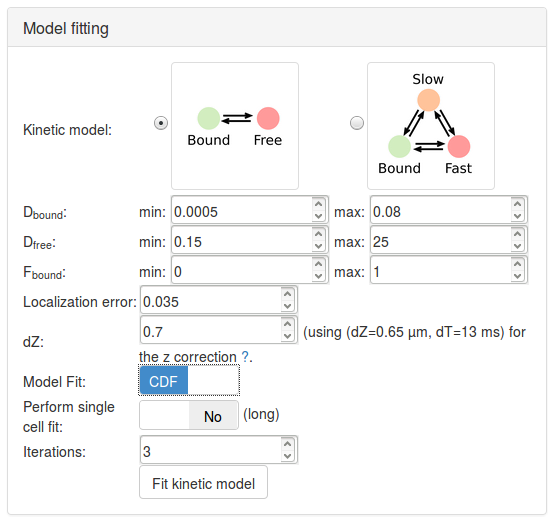
Having now reviewed the parameters, we can click the Fit kinetic model button. A "spinning wheel" will appear next to the button while the fit is being performed and will get displayed when the fit completes.
| Parameter | Value | Default? | Description/Comments |
|---|---|---|---|
| Kinetic model | 2-states model | N | |
| Dbound (µm²/s) | [0.005, 0.8] | Y | The range of diffusion coefficients for the bound fraction. |
| Dfree (µm²/s) | [0.15, 25] | Y | The range of diffusion coefficients for the free fraction. |
| Fbound | [0,1] | Y | The range for the fraction bound. |
| Localization error (µm) | 0.035 | Y | |
| dZ (µm) | 0.7 | Y | The estimated detection range in z. |
| Model Fit | CDF | N | Select whether the model will fit the jump length distribution (that is the probability density function, PDF), or the cumulative jump length distribution (CDF). |
| Perform single cell fit | No | Y | If "Yes", each individual dataset will be fit. Since our uploaded files are replicates of the same experiment, we want to pool them together. |
| Iterations | 3 | Y | The number of times the solver will independently be initialized. |
When adjusting the dZ and dT parameters (in the jump length distribution and the fitting parameters box, respectively, you will notice that the mention next to the dZ changes. The displayed values correspond to the closest pair of parameter for which a corrected \(Z\) depth has been derived -- corresponding to an \(Z\) depth adjusted for the possibility of particles exiting and entering the detection volume again (see the Methods section). The \(a\) and \(b\) parameters describe this corrected valued as a function of the estimated diffusion coefficient.
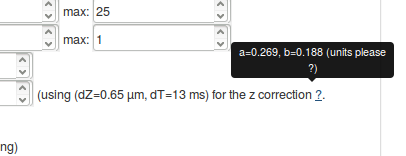
It is important to make sure that the set of displayed parameters is not too far from the real acquisition settings, else, the computed z correction might be wrong.
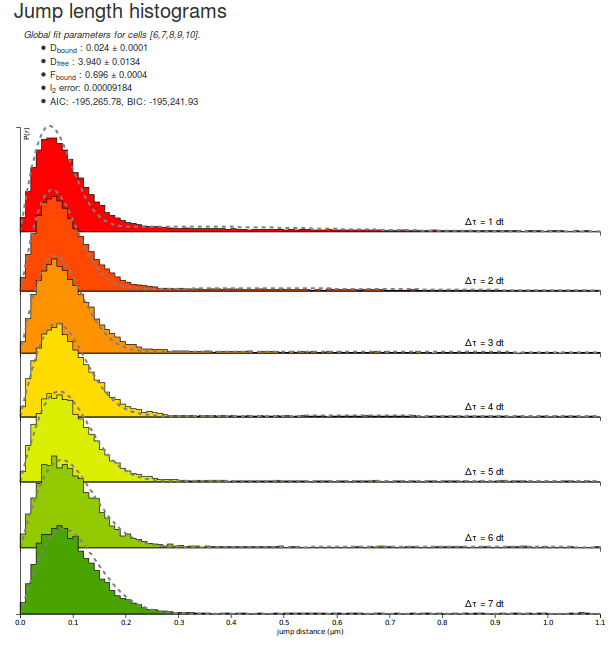
Let's take some time to quickly look at the parameters returned by the fitting routine for the H2B datasets. Note that due to different initialization values, the returned parameter can differ from execution to execution:
| Parameter | Value |
|---|---|
| Dbound | 0.024 µm²/s |
| Dfree | 3.940 µm²/s |
| Fbound | 0.696 |
| l2 error | 0.00009184 |
| AIC | -195265 |
| BIC | -195241 |
A few comments arise. First, the estimated fraction bound is about 70 %, which is expected from a strongly DNA-associated protein such as H2B. The associated coefficient with the bound population is close to zero (0.024 µm²/s) whereas the diffusion coefficient for the free population (3.94 µm²/s) matches previous knowledge of the dynamics of the protein.
Furthermore, the \(\ell_2\) error (the mean square error) is \(\lt 10^{-4}\), which can be considered as acceptable, even though significant misfit appear at low and high \(\Delta t\).
Finally, the AIC and BIC criterion are provided to allow model comparison. They cannot be used to assess the quality of fit per se. We will come back to those criteria later.
Step 9: mark the plot for download
Then, we can save the displayed fit by clicking the Mark for download button.
Step 10: fit the Sox2 dataset with a two-states model
We can now proceed similarly to derive the fit for the Sox2 datasets.
Step 11: fit a three-states model
Finally, we can now see how the quality of the fit increases by running the fit again, but with a 3-states model. Select the 3-state model icon (Slow-Bound-Fast) on the "Model fitting" box. New parameters appear, very similarly as with the two-states model. We will leave the parameters to their default values, except for the CDF fit. Then click the Fit kinetic model button and wait a until the fitting completes. Observe how the quality of fit evolves, and the parameters and estimated fractions.
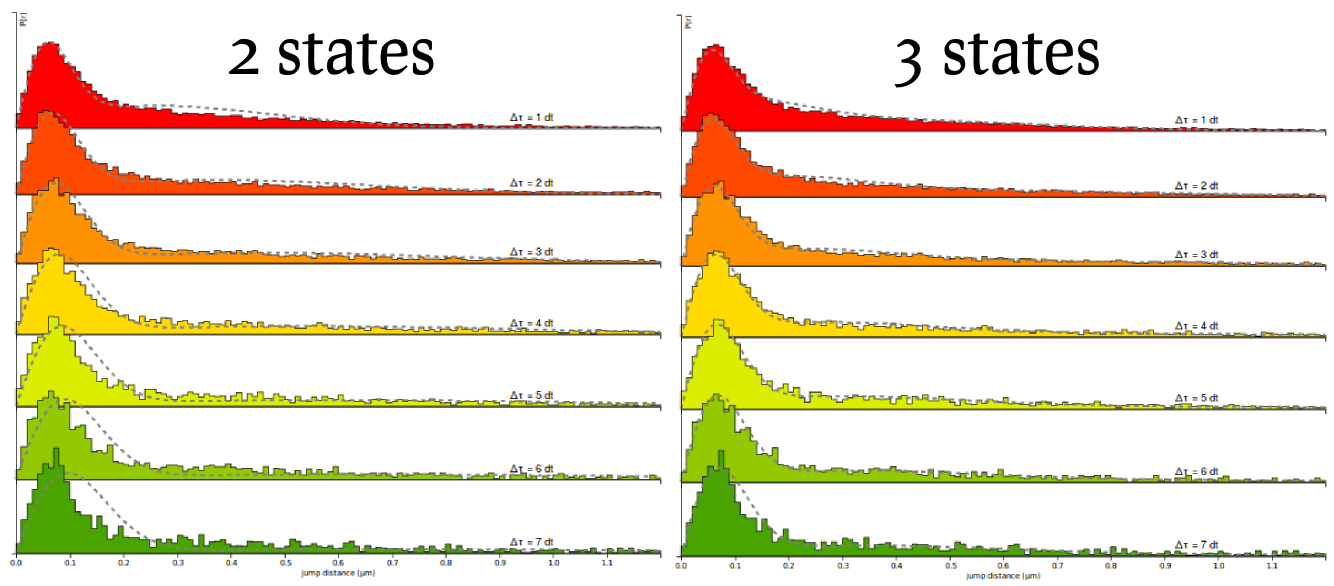
| Parameter | Value |
|---|---|
| Dbound | 0.037 µm²/s |
| Dfree | 2.747 µm²/s |
| Fbound | 0.337 |
| l2 error | 0.00043094 |
| AIC | -162789 |
| BIC | -162765 |
| Parameter | Value |
|---|---|
| Dbound | 0.014 µm²/s |
| Dslow | 0.643 µm²/s |
| Dfast | 4.938 µm²/s |
| Fbound | 0.244 |
| Fslow | 0.273 |
| l2 error | 0.00008137 |
| AIC | -197812 |
| BIC | -197772 |
Based on the information criteria, it is clear that the 3-states model provides a better fit to the data, even when penalizing for the number of parameters.
Download
Step 12: download the marked analyses
Finally move to the "Download" tab, where all the analyses we marked for download are stored. The view should look as below:
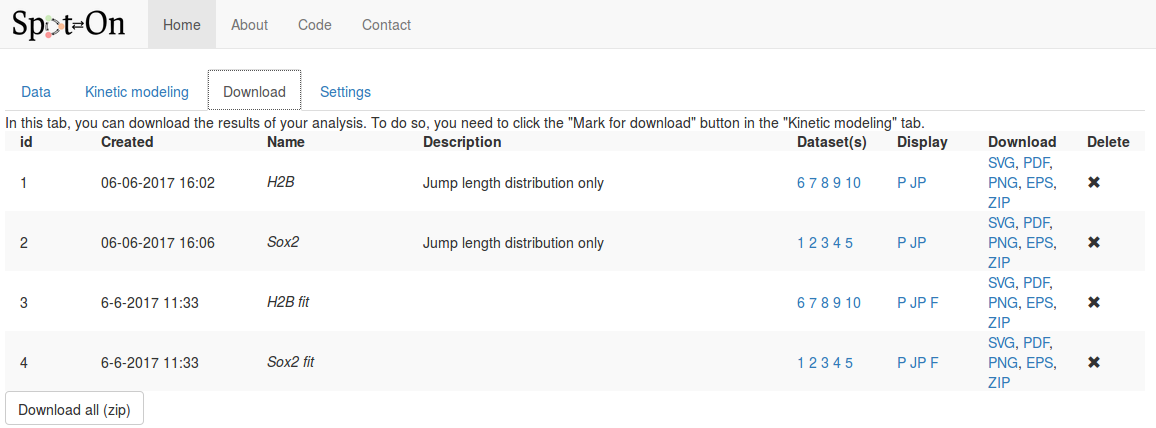
For each analysis marked for download, the following fields are displayed, in addition to the time of the analysis and the name and description we provided in the previous tab:
| Column | Description |
|---|---|
| Name & description | The name & description we provided in the previous tab. |
| Datasets | The list of datasets included for this plot. Hovering over the numbers displays the full name and description of the dataset. |
| Display | Codes corresponding to the type of plot displayed. Hover over the codes to see a short description:
P: display of the probability density function,
JP: display the pooled jump length distribution,
F: pooled fit displayed |
| Download | Download the corresponding analysis in various formats. The ZIP archive contains all the formats, the raw data, the display parameters and the fitted coefficients (if any). |
| Delete | To delete this analysis. |
Software reference
This section describes in detail the function of all the features and options implemented into Spot-On.
Input formats
Spot-On accepts tracking files from the following software and raw CSV (column naming below): TrackMate, MOSAIC suite. Sometimes, the importer can be a little bit picky. We provide sample files for these formats so that you can potentially study them. In case you have a problematic file, do not hesitate to contact us and email us the problematic file.
CSV (Comma-separated values)
Files can be uploaded as raw CSV files. Make sure that the separator indeed is a comma (,). Importing from a tab-separated or semicolon-separated file will not work. The CSV file should have a header line and contain the following columns. Any other column will be ignored. The order of the columns does not matter. Note that the header naming convention is case sensitive. This importer assumes that the tracking has been performes and that sets of detections were assigned a numerical index (or trajectory id).
| frame | t | trajectory | x | y | |
|---|---|---|---|---|---|
| Format | (integer) | (float) | (integer) | (float) | (float) |
| Description | Frame number | Time (in s) | The trajectory id | x position of the particle (in µm) | y position of the particle (in µm) |
TrackMate
TrackMate is an ImageJ/Fiji plugin that can perform various types of tracking and export the traces to various file formats. Spot-On can import from its XML and CSV export. Note that the file have to be exported from the last panel of the wizard (clicking the "Save" button at the bottom of the window will produce a XML file that cannot be read by Spot-On). A screenshot of TrackMate's export interface is displayed below.
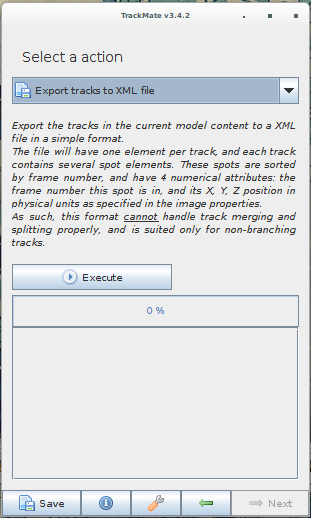
Again, the export can be performed by selecting either "Export tracks to a XML file" or "Export tracks to a CSV file". Clicking on "Save" will not work.
Download sample file (CSV) Download sample file (XML)UTrack
MOSAIC suite
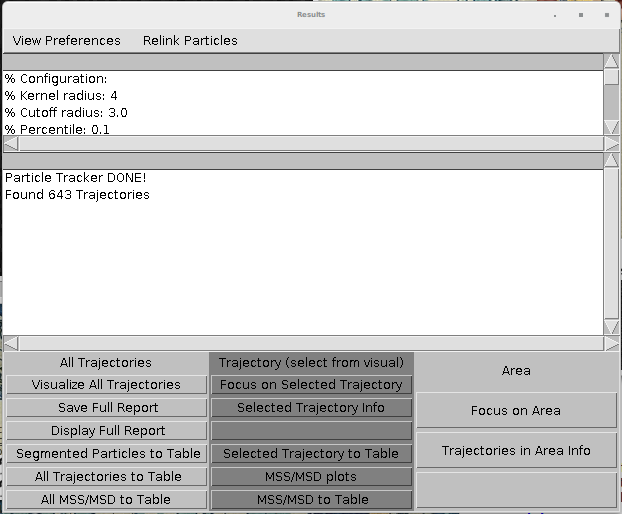
MOSAIC suite is an ImageJ/Fiji plugin that can perform tracking and export the traces an ImageJ table. This table can be further exported to CSV. The table is displayed by clicking the "All Trajectoried to table" and "Selected Trajectories to table" at the end of the wizard.
evalSPT
evalSPT (software mentioned in) produces a TSV format (tab-separated values), with no header (this is pretty bad), with the first columns ordered as follows. Additional columns might be present but will be ignored. An example file is provided below.
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 and more |
|---|---|---|---|---|
x position of the particle (in µm) |
x position of the particle (in µm) |
frame number | trajectory number | These columns are ignored |
Matlab file format
Spot-On also accepts a custom Matlab file format. An example is provided below. The trackedPar variable is a structured array. Each element of this array corresponds to one trajectory. Each trajectory contains several fields: xy, t, frame. Each of these fields is a 2D-matrix with 2, 1 and 1 columns, respectively and a number of rows corresponding to the number of detections for this trajectory.
Note that this format (in particulat the shape of the objects) has to be followed rigorously for Spot-On to be able to import it. In particular, a \(N\times 1\) matrix is different from a \(1\times N\) matrix.
Download sample fileImport codes
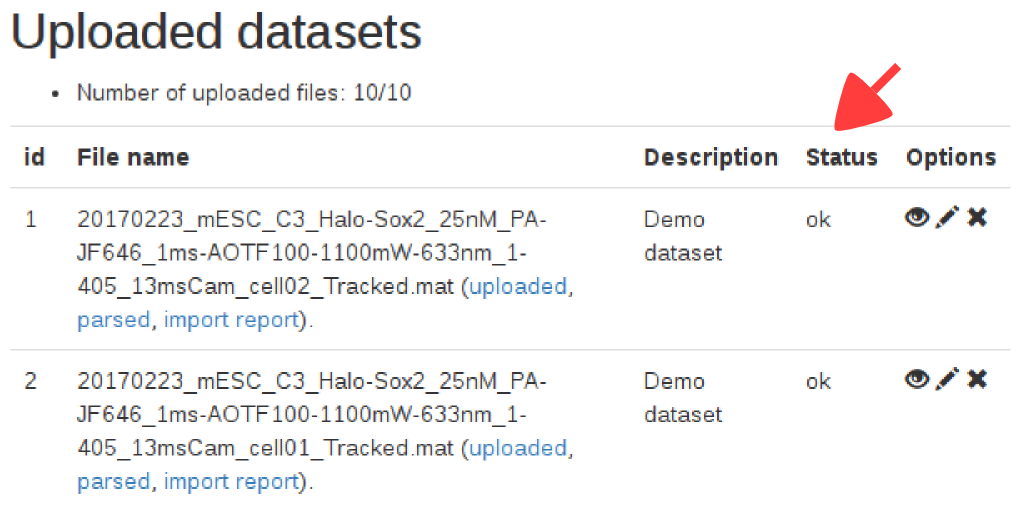
When a dataset is uploaded, a column "status" is displayed, showing the state of the import. Below is the meaning of the status codes displayed:| Status code | Meaning |
|---|---|
| Uploading | The dataset is being transferred to the server. |
| Queued | The dataset has been uploaded, and will be checked for import. |
| Ok | The dataset was successfully imported. |
| Error | Something went wrong with the import process, and the file could not be imported. The file has been deleted from our servers and you might want to check the file format and upload it again. |
Note that once the dataset is marked as "ok", the jump length distribution might still be computing in the background. The content of the second tab only appears when this computation is done, which might take a few seconds.
Dataset statistics
Once a dataset has been successfully imported, several statistics are displayed and allow you to get a quick overview of the data, and spot dubious datasets or datasets that might likely need to unreliable analyses. We detail below how theses statistics are computed and what are suggested reference values.
| Statistic | Meaning | Why it matters? |
|---|---|---|
| Number of traces | The number of trajectories in the dataset. Trajectories can be singletons (one detection) and arbitrary long. | A low number of traces is the sign of a dataset of poor quality? |
| Number of frames | The duration of the acquisition (in frames). This is inferred as the maximum index of the "frame" field. If you do not have detections at the end of the movie, this number can be lower than the true number of frames. | This number should more or less match the number of frames for the acquisition of this dataset. |
| Number of detections | The number of particles detected. | A low number of detections characterizes a dataset of low quality. Also, |
| Longest gap (frames) | The maximum number of frames during which a particle disappeared before being tracked again by the tracking software. | A number of gaps >2 frames is very likely to yield significant tracking errors. |
| Number of traces with ≥ 3 detections | Number of trajectories that contain three detections or more | This indicates whether histograms can be populated for \(\Delta t > 1\). |
| Number of jumps | The number of tracked translocations | Jumps are used to build the histogram of jump lengths, this is probably one of the most relevant metric to evaluate the quality of the dataset. |
| Length of trajectories (in number of frames) | Provides the mean and median length of trajectories. | |
| Particles per frame | The mean and median number particles per frame. | A median number higher than one indicates the risk of tracking errors. |
| Jump length (µm) | The mean and median translocation distance | This number has to be compared to the pixel size and has to remain relatively low to minimize the risk of tracking error. To keep it low, a way is to increase the framerate. |
Jump length distribution computation parameters
The empirical jump length distribution is computed according to several parameters that are detailed below.| Parameter | Meaning | Why it matters? |
|---|---|---|
| Bin width (µm) | how finely to do binning for PDF fitting and plotting in units of micrometers. Generally 0.010 μm or 10 nm is reasonable, but if you have very small amounts of data you may want to increase it. | |
| Number of timepoints | How many time points to consider. If you allow \(N\) time points, this corresponds to considering displacements with a maximal time-delay of \((N-1)\Delta t\). Generally, we do not recommend going much above 50-60 ms unless you have an a very large number of trajectories and/or very long trajectories, since otherwise, the displacement histograms at longer \(\Delta t\) tend to be undersampled. | |
| Jumps to consider | The first Jumps To Consider+Number of time points - 4 displacements will be considered. e.g. if JumpsToConsider=4 and TimePoints=8 and the present trajectory was 10 frames, only the first 8 displacements or 9 frames
will be considered. The trajectory will then contribute 8
displacements to the \(1\Delta t\) histogram, 7 displacements to the \(2\Delta t\)
histogram, ..., and 2 displacements to the \(7\Delta t\) histogram. This parameter is ignored if "Use all trajectories" is set to Yes. |
|
| Use all trajectories? | If "Use all trajectories" is set to "Yes", the previous parameter ("Jumps to consider" is being ignored. If set to "Yes", all displacements will be used from each trajectory. If set to "No", then the number of displacements is determined by the "Jumps to consider" variable. A trajectory of \(N\) frames, will contribute \(N-1\) displacements to the \(1\Delta t\) histogram, \(N-2\) displacements to the \(2\Delta t\), histogram, ..., \(N-k\) displacements to the \(k\Delta t\) histogram. | |
| Max jump (µm) | this parameter affects data-processing. For binning displacements, a maximum displacement has to be set, so this parameter should be set to a large value that should be at least as big as the largest displacement. Generally, 5.05 μm is reasonable for single-molecule tracking data in mammalian cells. | |
| dT (ms) | Time delay between frames in units of milliseconds. |
Fitting parameters
| Parameter | Meaning | Why it matters? |
|---|---|---|
| Kinetic model | The number of diffusive states in the model. Spot-On supports 2- or 3-states. In most single-molecule tracking experiments of molecules that can engage scaffolds (e.g. transcription factors, which may bind chromatin), one of these states will correspond to a bound state. In the case of Halo-CTCF in human U2OS cells, this will manifest itself as the chromatin-bound state of CTCF exhibiting a very small \(D\) for the bound state which likely corresponds to slow diffusion of chromatin. The other states will correspond to freely diffusive states. | |
| Dfree, Dbound, Dslow, Dfast | Allowed lower and upper bound for the faster diffusion constant for the model-fitting in units of μm²/s for the free (2-states model), bound (all models), slow (3-states model) or fast (3-states model), respectively. | |
| Fbound, Ffast | The range of possible values for the bound fraction (all models) and the fast-diffusing fraction (3-states model), respectively. | |
| Localization error (µm) | If "Fit from data" is set to "No", you can provide the localization error with which single-molecules were localized. If "Fit from data" is set to "Yes", Spot-On will try to infer this from the model-fitting. In that latter case, you need to provide an exploration range for these values. In the datasets provided with Spot-On, the localization error was around 35 nm. If the localization error parameter is set inaccurately, this will generally show up through poor fitting of the bound state and will cause the estimation of the bound diffusion constant to be inaccurate. | |
| dZ (µm) | Axial observation slice in units of micrometers. This parameter will depend somewhat on signal-to-noise conditions and imaging modality. But for a typical setup (HiLo or epi illumination, HaloTag or SNAP-Tag dyes), this is likely to be around 0.7 μm. The parameters tell Spot-On how far out-of-focus a molecule can be before it fails to be detected and it is important for accurately correcting for diffusing molecules gradually moving out-of-focus and thus being undersampled at longer time-intervals. In most cases 0.7 μm is reasonable, but for details on how to measure this please see (Hansen et al. (2017). | |
| Perform single cell fit | When set to "Yes", each single uploaded file will be analyzed and fitted separately. This is useful for assessing how much cell-to-cell variability there is and for determining whether a single outlier is biasing the results, but also very slow, since fitting merged data takes about the same amount of time as fitting a single cell. | |
| Model Fit | Determines whether fitting will be performed to the displacement histograms (PDF) or to the cumulative distribution function of displacements (CDF). We have performed Monte Carlo simulations and CDF-fitting is always more precise, whereas PDF-fitting tends to slightly underestimate the fraction bound and the diffusion constant, likely because PDF-fitting is more prone to binning artifacts and undersampling. Thus, for all quantitative analysis, CDF-fitting should be performed. However, displacement histograms often seem more intuitive, and for this reason Spot-On also allows PDF-fitting for making figures etc. | |
| Iterations | Spot-On fits a mathematical model to the data using least-squares fitting. Since this algorithm may occasionally get trapped in local minima in parameter space, for each iteration of the fitting Spot-On generates a random initial guess of the parameters, which differs between each iteration. Thus, increasing the "Iterations" parameter, increases the probability that the globally optimal fit will be generated, but comes at the cost of slowing down the fitting. In practice, for all single-molecule tracking data we have tested so far, the globally best fit is always obtained in the first or second iteration of fitting, so we generally recommend keeping this parameter to 2-3. |
Display parameters
These parameters affect how the graphs are displayed, and which features are to be plotted. It does not affect how the fits or the jump length distribution are computed. These settings are located under the graph region.
These parameters are only displayed when a graph has been processed. This is either done automatically after datasets have been successfully uploaded or by clicking the "Compute!" button in the "Jump length distribution parameters" box. Some of the settings only appear for specific settings.
| Parameter | Meaning | Only displayed if... |
|---|---|---|
| Max jump displayed (µm) | The range of distances to be plotted. This parameter varies between 0 µm and "Max Jump". It allows to zoom on the origin of the plot. | For any plot |
| Display PDF/CDF | Either display the PDF or the CDF | For any plot. |
| Show pooled jump length distribution | Tell whether single datasets should be displayed or if the selected datasets should be pooled together. | For any plot. |
| Displayed group | The list of datasets displayed in the pooled graph | Show pooled jump length distribution is set to "Yes" |
| Display dataset | Sets the dataset to be displayed | Show pooled jump length distribution is set to "No" |
| Show pooled fit | Tell whether fit for individual datasets or the fit for all the selected datasets has been computed | a fit has been computed |
| Display residuals | If set to "Yes", the residual between the fit and the empirical jump length distribution is overlaid on the graph. | a fit has been computed |
| Mark for download | This button allows to mark the current plot for download. When doing so, all the current settings are saved and will be available in the download section. You have the possibility to add a few annotations to the download for easier sorting. | For any plot |
How to acquire a "good" dataset?
Methods
Spot-On extracts kinetic parameters by fitting the jump length distribution of the tracked particles while taking into account that a significant fraction of the particles might be moving out of focus during the imaging process. This approach is based on the initial work by Mazza et al. (2012), further simplified by Hansen et al. (2017).
Outline of the method
Transcription factors (or DNA-binding factors in general) can be envisioned (in an over-simplified manner) as proteins alternating between several states in the nucleus:
- One "freely diffusing" state, where the diffusion of the factor is governed by its interactions with the nuclear components
- One "bound" state, where the factor is immobilized onto chromatin
In this context, identifying the fraction of proteins present in each state and and its diffusion coefficient is of biological relevance.
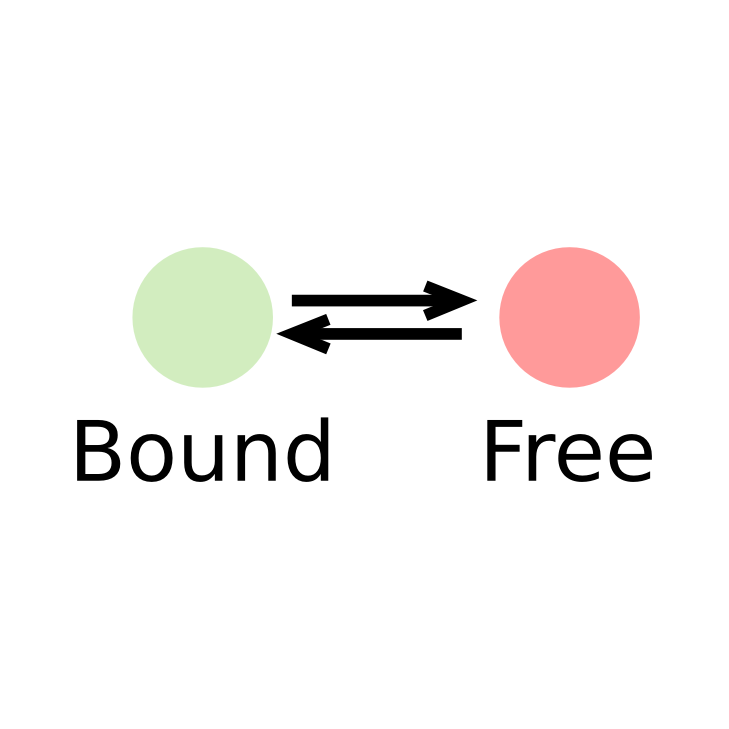
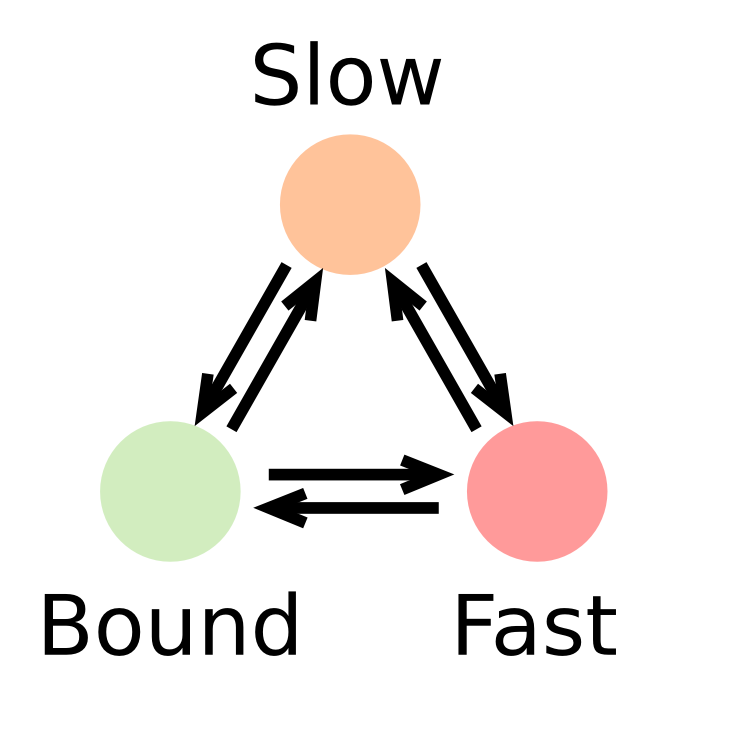
In such a context, the kinetic parameters mentioned above (fraction of the observed population and diffusion coefficient of each of the states) can be inferred by fitting a model to the histogram of jump lengths derived from single particle data (SPT). In an histogram of jump lengths, several populations can overlap with various diffusion coefficients. The slow-moving fraction tends to show short displacements, possibly dominated by localization error while the fast-moving fraction shows bigger jumps. Such fractions can be estimated using adequate modeling.
Such model has to account for two extra parameters: localization error and particles moving out of focus.
Derivation of the two states kinetic model
The evolution over time of a concentration of particles located at the origin as a Dirac delta function and which follows free diffusion in two dimensions with a diffusion constant \(D\) can be described by a propagator (also known as Green’s function). Properly normalized, the probability of a particle starting at the origin ending up at a location \(r = (x,y)\) after a time delay, \(\Delta t\), is then given by:
$$P(r, \Delta t) = N \frac{r}{2D\Delta t}e^{-\frac{r^2}{4D\Delta t}}$$Here, \(N\) is a normalization constant with units of length. In practice, this distribution is compared to binned data: we integrate this distribution over a small histogram bin window \(\Delta r\), to obtain a normalized distribution and to compare to the empirically measured distribution. For simplicity, we therefore leave out this normalization constant of subsequent expressions.
Furthermore, in practice, we are unable to determine the precise localization of a single molecule. Instead, it is associated with a certain localization error \(\sigma\). Correcting for localization errors is important because it will other- wise appear as if molecules move further between frames than they actually did. Thus, we obtain the following expression for the jump length distribution taking localization error, \(\sigma\), into account (Matsuoka et al., 2009)
$$P(r, \Delta t) = \frac{r}{2\left(D\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D\Delta t + \sigma^2\right)}}$$Next, we assume that the protein of interest exists in two states, one bound (characterized by a specific diffusion coefficient, \(D_{bound}\), and a fraction bound, \(F_{bound} \in [0,1]\)) and one "free" (characterized by a specific diffusion coefficient, \(D_{free}\), and a fraction free, \(F_{free} = 1-F_{bound}\)). Thus, the distribution of jump length \(P(r, \Delta t)\) reflects this mixture of two populations:
$$P(r, \Delta t) = F_{bound} \frac{r}{2\left(D_{bound}\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{bound}\Delta t + \sigma^2\right)}} + \left(1-F_{bound}\right)\frac{r}{2\left(D_{free}\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{free}\Delta t + \sigma^2\right)}}$$Then, fast-moving molecules are more likely to move out of the focal plane or axial detection window (\(\Delta z\)) during 2D image acquisition than slow-moving or bound molecules. Even though for short lag times (e.g \(\Delta t \sim 5-30 \text{ ms}\)), this is still long enough for a large fraction of the free population to be lost. As a consequence, bound molecules tend to have much longer trajectories than do free molecules. Again, this means that we are oversampling the bound population and undersampling the free population.
To correct for this, we consider the probability that a freely diffusing molecule with diffusion constant \(D_{free}\) will move out of the axial detection window \(\Delta z\) during a lag time \(\Delta t\). This problem has also been previously considered (Kues and Kubitscheck, 2002). If we consider the extreme case of a population of molecules equally distributed one-dimensionally along an axis \(z\), with an absorbing boundary at \(z_{max} = \Delta z/2\) and \(z_{min} = -\Delta z/2\), the fraction \(P_{remaining}\), of molecules remaining at lag time \(\Delta t\), is given by:
$$P_{remaining}(\Delta t) = \frac{1}{\Delta z}\int_{-\Delta z/2}^{\Delta z/2} \left\{ 1-\sum_{n=0}^{\infty}(-1)^n \left[ \text{erfc}\left(\frac{\frac{(2n+1)\Delta z}{2}-z}{\sqrt{4D_{free}\Delta t}} \right) + \text{erfc}\left(\frac{\frac{(2n+1)\Delta z}{2}+z}{\sqrt{4D_{free}\Delta t}} \right) \right]\right\}dz$$However, this expression significantly overestimates how many freely diffusing molecules are lost since it assumes absorbing boundaries: any molecules that comes into contact with the boundary at \(\pm \Delta z/2\) are permanently lost. In reality, there is a significant probability that a molecule, which has briefly contacted or exceeded the boundary, re-enters the axial detection window, \(\Delta z\), during a lag time \(\Delta t\). Moreover, since trajectory gaps can be allowed in the tracking algorithm (i.e. a molecule present in frame \(n\) and \(n+2\) can still be tracked even if it was not localized in frame \(n+1)\), we must consider the probability that a lost molecule re-enters the axial detection window during twice the lag time, \(2 \Delta t\). This results in the somewhat counter-intuitive effect, which was also noted by Kues and Kubitscheck, that the decay rate depends on the microscope frame rate. In other words, the fraction lost depends on how often one 'looks'. One approach (Mazza et al., 2012) of accounting for this is to use a corrected axial detection window larger than the true axial detection window: \(\Delta z_{corr} > \Delta_z\).
\(\Delta z_{corr}\) was computed from the true \(\Delta z\) as:
$$\Delta z_{corr}(\Delta z, \Delta t, D) = \Delta z + a(\Delta z, \Delta t)\sqrt{D} + b(\Delta z, \Delta t)$$where compute the coefficients \(a\) and \(b\) were fitted based on Monte Carlo simulations. Indeed, for a given diffusion constant, \(D\), 50,000 molecules were uniformly placed one-dimensionally along the z-axis from \(z_{min} = -\Delta z/2\) to \(z_{max} = \Delta z/2\). Next, using a time-step \(\Delta t\), we simulated one-dimensional Brownian diffusion along the z-axis. For time gaps from \(1 \Delta t\) to \(15 \Delta t\), we calculated the fraction of molecules that were lost, allowing for one missing frame as the default setting in our tracking algorithm. We repeated these simulations for particles with diffusion constants in the range of \(D = 1 \mu\text{m}^2/s\) to \(D = 12 \mu\text{m}^2/s\) to generate a comprehensive dataset over a range of biologically plausible diffusion constants. From this series of simulation, a pair of coefficients \(\left(a(\Delta z, \Delta t), b(\Delta z, \Delta t) \right)\) was estimated. The process was repeated over a grid of plausible values of \((\Delta z, \Delta t)\) to derive a grid of \((a,b)\) parameters.
Having derived an analytical expression for the probability of a free molecule being lost due to axial diffusion during the imaging time, we can now thus write down the final equations used for fitting the raw jump length distributions:
$$P(r, \Delta t) = F_{bound} \frac{r}{2\left(D_{bound}\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{bound}\Delta t + \sigma^2\right)}} + Z_{corr}(\Delta t)\left(1-F_{bound}\right)\frac{r}{2\left(D_{free}\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{free}\Delta t + \sigma^2\right)}}$$where:
$$Z_{corr}(\Delta t) = \frac{1}{\Delta z}\int_{-\Delta z/2}^{\Delta z/2} \left\{ 1-\sum_{n=0}^{\infty}(-1)^n \left[ \text{erfc}\left(\frac{\frac{(2n+1)\Delta z_{corr}}{2}-z}{\sqrt{4D_{free}\Delta t}} \right) + \text{erfc}\left(\frac{\frac{(2n+1)\Delta z_{corr}}{2}+z}{\sqrt{4D_{free}\Delta t}} \right) \right]\right\}dz$$Finally, some questions arise about how to build the empirical jump length distribution.
One of them is whether to use the entire trajectory or not. One bias against moving molecules is that frequently, freely diffusing molecules will translocate through the axial detection window, \(\Delta z\), yielding only a single detectable localization and thus no jumps to be counted. Conversely, one bias against bound molecules, is that moving molecules can re-enter the axial detection window multiple times resulting in the same molecule appearing as multiple distinct trajectories and thus being over-counted. Clearly, the extent of the bias will depend on the photobleaching rate – in the limit of no photobleaching, a single freely diffusing molecule could yield a very high number of different trajectories, leading to large over-counting of the free population. However, in practice, using the current dyes and high laser illumination, the average dye lifetime is quite short. Thus, the number of jumps to consider should be chosen accordingly with the estimated diffusion coefficient and the exposure time.
Another free parameter is the number of \(\Delta t\) used to fit the model. The default parameter is 7 \(\Delta t\), but this has to be adjusted so that the histograms for the longer time intervals remain populated.
Generalization to a 3-states model
Having introduced the theory for the inference of a two-states kinetic model, derivation of a three-states is straightforward.
First, we assume that the observed factor exists in three distinct populations, characterized by their diffusion coefficients \(D_{bound}\), \(D_{slow}\), \(D_{fast}\) and by their fractions: \(F_{bound}\), \(F_{slow}\), \(F_{fast}\), and the relationship \(F_{bound}+F_{slow}+F_{fast}=1\) holds, describing a model with five free parameters. From that, we can derive the (uncorrected) jump length distribution \(P_3(r, \Delta t)\):
$$\begin{align} P_3(r, \Delta t) = & F_{bound} \frac{r}{2\left(D_{bound}\Delta t \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{bound}\Delta t + \sigma^2\right)}}\\ + & F_{slow} \frac{r}{2\left(D_{slow}\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{slow}\Delta t + \sigma^2\right)}}\\ + &\left(1-F_{bound}-F_{slow}\right)\frac{r}{2\left(D_{fast}\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{fast}\Delta t + \sigma^2\right)}} \end{align}$$Then, as described in the two states model, this derivation is biased against fast-moving molecules, that tend to move out of focus whereas slow-moving and bound molecules remain in the focal plane for more frames. This results into slow-moving molecules exhibiting more jumps than the fast moving molecules. This distribution is thus corrected by a factor taking into account the fraction of molecules lost by moving out of focus:
$$\begin{align} P_3(r, \Delta t) = & F_{bound} \frac{r}{2\left(D_{bound}\Delta t \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{bound}\Delta t + \sigma^2\right)}}\\ + & Z_{corr}(\Delta t, D_{slow})F_{slow} \frac{r}{2\left(D_{slow}\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{slow}\Delta t + \sigma^2\right)}}\\ + & Z_{corr}(\Delta t, D_{fast})\left(1-F_{bound}-F_{slow}\right) \frac{r}{2\left(D_{fast}\Delta t + \sigma^2\right)}e^{-\frac{r^2}{4\left(D_{fast}\Delta t + \sigma^2\right)}} \end{align}$$where \(Z_{corr}(\Delta t, D)\) is unchanged compared to the two-states model:
$$Z_{corr}(\Delta t, D) = \frac{1}{\Delta z}\int_{-\Delta z/2}^{\Delta z/2} \left\{ 1-\sum_{n=0}^{\infty}(-1)^n \left[ \text{erfc}\left(\frac{\frac{(2n+1)\Delta z_{corr}}{2}-z}{\sqrt{4D_{free}\Delta t}} \right) + \text{erfc}\left(\frac{\frac{(2n+1)\Delta z_{corr}}{2}+z}{\sqrt{4D_{free}\Delta t}} \right) \right]\right\}dz$$Asumptions of the approach
This modeling approach makes the following asumptions. In case those asumptions are not fullfilled, the result can be unreliable. Or total garbage. Or a Gremlins can jump out of your screen. Who knows.State changes are neglected
The modeling approach described above does not explicitely incorporate the exchange rates between the different states (the apparent \(k^*_{on}\) and \(k_{off}\)), but defines rather the fraction in each of the states, and assumes that:
$$F_{bound} = \frac{k^*_{on}}{k^*_{on}+k_{off}}$$However, our approach assumes that state exchange is rare when compared to the imaging framerate: that is that one observed jump likely belongs to one molecule either in one state or the other, rather than an average between the two states due to state exchange. May this asumption be violated, then the estimate of diffusion coefficients and fraction bound might be wrong.
The correction for particles that move out of focus is semi-empirical
Although an analytical formula exists to estimate the fraction of molecule that reach the limit of the detection volume after a time \(\Delta t\), this formula does not take into account the fact that molecules can exit the detection volume for a very short time, or can exit for the duration of ~ 1 frame and reenter one frame later, a behaviour that can be captured if the tracking algorithm is configured to allow for a gap. To take into account those effects, the corrected detection volume \(\Delta z_{corr}\) is estimated from Monte Carlo simulations. Spot-On relies on a database of ~16000 Monte Carlo simulations for a wide range of \(\Delta t, \Delta z, D\) values. Several limitations apply:
- For values of \(\Delta t\) and \(\Delta z\) kept constant, we assume that \(\Delta z_{corr}\) follows the empirical relationship: \(\Delta z_{corr} = \Delta z + a\sqrt{D} + b\). This fit might not be accurate for all pairs of parameters.
- All the Monte Carlo simulations were performed with the tracking algorithm allowing for one gap frame. Thus, these values might be inaccurate for higher or lower number of gaps.
Numerical implementation
Here is a little bit more details about how this model is implemented and fitted into Spot-On.
Computation of the jump length distribution
The empirical jump length distribution is computed as follows: first, the MaxJump and BinWidth parameters determine the range to build the histogram, and ulitmately the number of bins it will contain. Also, the input file is filtered for trajectories that contain more than three localizations.
Then, the histogram in itself is built. For each trajectory, the JumpsToConsider parameter determines how many of the first jumps will be taken into account for the building of the histogram. If the UseAllJumps is set to "Yes", then all jumps (and not the first few ones) will be used to build the histogram. Note that this later option is likely to bias the histogram towards bound molecules. For this procedure, the number of gaps in the data is extracted.
To increase the robustness of the fit, several histograms are built with increasing time lags \(\Delta t\). The number of histograms to be built is determined by the Number of time points parameter.
Computation of the model
The model presented above can be numerically evaluated. To do so, one has to compute one 1D numerical integration and one infinite sum. The integral is computed using the midpoint method over 200 points. The terms of the series are computed until the term falls below a \(10^{-10}\) threshold.Fitting
Parameter optimization of \((D_{free}, D_{bound}, F_{bound})\) (or \((D_{fast}, D_{slow}, D_{bound}, F_{fast}, F_{bound})\) for a 3-states model) is performed using a non-linear least-square algorithm. In practice, the
Levenberg-Marquardt solver implemented wrapped by the lmfit library is used. User-provided bounds are enforced and the algorithm provides estimates of the uncertainty for each estimated parameter. The routine is initialized with parameters drawn uniformly from the specified parameter range. The optimization is repeated several times with different initialization parameters. This number of initializations is determined by the Iterations parameter.
Specificities for the fitting of the three-states model
The three-states model is fitted similarly as the two-states model. The only difference is the parameter bounds cannot be easily specified. Indeed, the optimization is performed under the following constraints:
$$\begin{align} D^{MIN}_{bound} \leq D_{bound} \leq D^{MAX}_{bound} \\ D^{MIN}_{slow} \leq D_{slow} \leq D^{MAX}_{slow} \\ D^{MIN}_{fast} \leq D_{fast} \leq D^{MAX}_{fast} \\ 0 \leq F_{bound} \leq 1\\ 0 \leq F_{slow} \leq 1\\ 0 \leq F_{fast} \leq 1\\ F_{bound} + F_{slow} + F_{fast} = 1 \end{align}$$The first six constraints are easy to enforce since they constrain the optimization inside an hypercube, and is built-in the solver. However, the last constraint, \(F_{bound} + F_{slow} + F_{fast} = 1\) is a triangular constraint for which a specific cost function was written. Indeed: \(F_{bound} + F_{fast} \leq 1\). Thus the cost function was modified to penalize parameters sets where \(F_{bound} + F_{fast} > 1\).
In practice, denoting \(X_i, i \in [0,N]\) the bins of the empirical histogram with \(N\) the number of bins (\(N = \lfloor \frac{\text{MaxJump}}{\text{BinWidth}}\rfloor\), and \(X^*_i, i \in [0,N]\) the model resulting a set of candidate parameters, the algorithm minimizes the cost function \(L(X,X^*)\):
$$L(X,X^*) = \sum_{i=0}^N \left(X_i-X^*_i\right)^2 + 10^4\left(F_{bound}+F_{fast}-1\right)\mathbf{1}_{F_{bound} + F_{fast} > 1}$$where \(\mathbf{1}\) denotes the indicator function. This in practice constrains the optimization to the half-plane where \(F_{bound} + F_{fast} \leq 1\).
References
Mazza, D., A. Abernathy, N. Golob, T. Morisaki, and J. G. McNally. “A Benchmark for Chromatin Binding Measurements in Live Cells.” Nucleic Acids Research 40, no. 15 (August 1, 2012): e119–e119.
-
Hansen, Anders S., Iryna Pustova, Claudia Cattoglio, Robert Tjian, and Xavier Darzacq. “CTCF and Cohesin Regulate Chromatin Loop Stability with Distinct Dynamics.” Elife 6 (2017).
-
Matsuoka, Satomi, Tatsuo Shibata, and Masahiro Ueda. “Statistical Analysis of Lateral Diffusion and Multistate Kinetics in Single-Molecule Imaging.” Biophysical Journal 97, no. 4 (August 2009): 1115–24.
-
Kues, Thorsten, and Ulrich Kubitscheck. “Single Molecule Motion Perpendicular to the Focal Plane of a Microscope: Application to Splicing Factor Dynamics within the Cell Nucleus.” Single Molecules 3, no. 4 (2002): 218–24.
Code
Spot-On is a free/open-source software, feel free to contribute by reporting bugs, helping us to write the documentation or proposing new features. The code of Spot-On is available on the software forge GitLab, in the Spot-On repository. A bugtracker is also available for bug reports and feature requests.

Spot-On is divided in several packages:
- The web-interface
- The command-line backend, that can be used standalone and offline
- A Matlab© backend
The web-interface is released under the AGPL license. The backend is released under the GNU GPL version 3+
Datasets
Frequently asked questions
What is Spot-On?
Spot-On is an online tool to extract kinetic parameters from fast single particle tracking experiments. It does it in a manner that takes into account the finite depth of field of the objective and proposes corrections for that. Spot-On can fit two-states (Bound-Free) and three-states (Bound-Free1-Free2) models.
Spot-On takes a set of trajectories as input (multiple formats supported) and outputs a fitted jump length distribution, together with goodness-of-fit metrics and the corresponding fitted coefficients.
What is not Spot-On?
Spot-On is not a tracking algorithm, thus you need to perform the tracking of your single particle tracking datasets using a separed algorithm. Spot-On accepts inputs from a range of popular tracking softwares, and you can either add your own or write a converter towards a standard table-file import.
What tracking software to use?
What type of input Spot-On accepts?
See this section of the documentation.
My input format does not seem to be supported, what can I do?
If the format of the tracking algorithm you use is not supported by Spot-On, here are a few things you can try:
- If you believe that this format should be added to Spot-On, feel free to contact us, either through our contact page or by creating an issue on our Gitlab bugtracker.
- Meantime, you can try to convert your file to one of the formats supported by Spot-On. A description of the formats supported by Spot-On is presented above. For instance, the CSV format has a very simple syntax.
- If you have programming skills, feel free to write an importer! The structure of the parser is documented in the
/SPTGUI/parsers.pyfile. Do not forget to open an issue on the bugtracker so that we are aware that you are working on a specific file format.
How fast is Spot-On?
During our tests that included up to 1 million detections, the computation of the jump length distribution and the fitting of the most complicated kinetic model (3 states with estimation of the localization error from the data) usually takes about one minute.
That said, the fitting speed depends on many parameters (load of the server, range of the parameters, shape of your jump length distribution, etc). If the online version of Spot-On is performing too slowly for your needs, feel free to get either the offline version of Spot-On, or the command line version.
Are you just fitting a two-exponential model?
This is slightly more complicated, for several reasons presented in details in the methods section:
- Spot-On can perform both two- and three-populations fitting
- Spot-On can estimate the localization error from the data
- As fast populations tend to move out of focus more than bound molecules, the estimate of the fraction of the molecules in each state is usually heavily biased towards slow-moving particles. Spot-On implements a previously-published semi-empirical correction to account for that.
- Spot-On implements quality checks to warn the user when the uploaded datasets seem to show inconsistencies or were performed in conditions that might lead to unreliable parameter estimation.
I'm afraid of uploading my dataset to your server. Is there an offline version?
Sure! Spot-On is fully free/open-source and detailed download and installation instructions can be retrieved from our Gitlab page.
Is there a command-line version?
There is! Spot-On uses an independent command-line Python backend that is available in our Github repository. It implements most of the features of Spot-On, comes with simple wrapper functions that can quickly be implemented in your scripting framework.
What technology uses Spot-On?
Spot-On is written in Python. The backend relies on the lmfit library. The server is based on Django and uses Celery to run an asynchronous queue to perform jobs. The frontend is written in AngularJS and the graphs are rendered through D3.js.
Is there a Matlab® version?
There is! Check this page (to be updated soon, contact us to get the version as soon as we release it).
What license uses Spot-On?
Spot-On is two-folds:
- The fitting backend is released under the GNU General Public License version 3 or higher. You can consult one of these links for a summary of the license: [1] [2].
- The server frontend, that wraps the fitting backend is released under the GNU Affero General Public License version 3 or higher. You can consult one of these links for a summary of the license: [1] [2].
I have a question
We'd love to hear it! You can either:
- Contact us by email (using our contact form)
- Open an issue on our Gitlab bugtracker
How do you handle privacy?
We only collect minimal information when you upload your datasets (your IP is saved somwhere in the logs but we don't use it), we do not ask for email or identification: no account is required to use Spot-On. Furthermore, you can erase your analysis anytime by going to the Settings tab in the analysis page. Finally, we provide an offline and a command-line version that you can run on your own machine. If you have any concern, feel free to write to us.
How to cite Spot-On?
We've no idea so far!
How to contact you?
We have a contact form. You will receive a copy of your message and we will then communicate by email.
I found a bug, how can I report it?
Thanks a lot for letting us know, this is really important to us! You can either open an issue on our Gitlab bugtracker or drop us a message.